Outlier detection - a review of different approaches

“Il est impossible que l’improbable n’arrive jamais” -- Emil Gumbel

An outlier is an observation that diverges (i.e. it is distant) from other observations in a sample.
Outliers are also referred to as observations whose probability to occur is low.

Outliers can impact the results of analysis and statistical modelling, by altering the relationship between variables.
However, when trying to detect outliers in a dataset it is very important to keep in mind the context.

Indeed, unusual observations are not necessarily outliers; in some cases, they are legitimate observations that accurately describe the variability in the data and may contain valuable information.

Even if determining whether or not an observation qualifies as an outlier is necessarily a subjective matter, several approaches and techniques can come to the aid.

Outliers Detection Techniques

Different approaches can be adopted to detect anomaly observations:

•   univariate approach, in which a single variable is analysed

•  multivariate approach, in which more than one variable are analysed at the same time

•   parametric approach, which involves statistical metrics based on parameters of the feature’s distribution

•   non-parametric approach

Some of the most popular methods for outlier detection are:

•    Extreme Value Analysis
•    Probabilistic and Statistical Modelling
•    Linear Regression Modelling
•    Proximity-Based Models

• Extreme Value Analysis: this is a univariate parametric approach which qualifies as outliers those values which are too large or to small compared to some threshold defined on the basis of some parameter’s distribution, such as the Z-scores or the Tukey’s IQR – Interquartile Range.

The Z-scores approach quantifies the unusualness of an observation in terms of how many standard deviations a data point is from the sample’s mean, assuming a gaussian distribution.
For any data point , its zi-score can be calculated by subtracting the mean and dividing by the standard deviation as follows

The further away an observation’s z-score is from zero (above or below), the more unusual it is. The probability distribution below displays the distribution of Z-scores in a standard normal distribution.

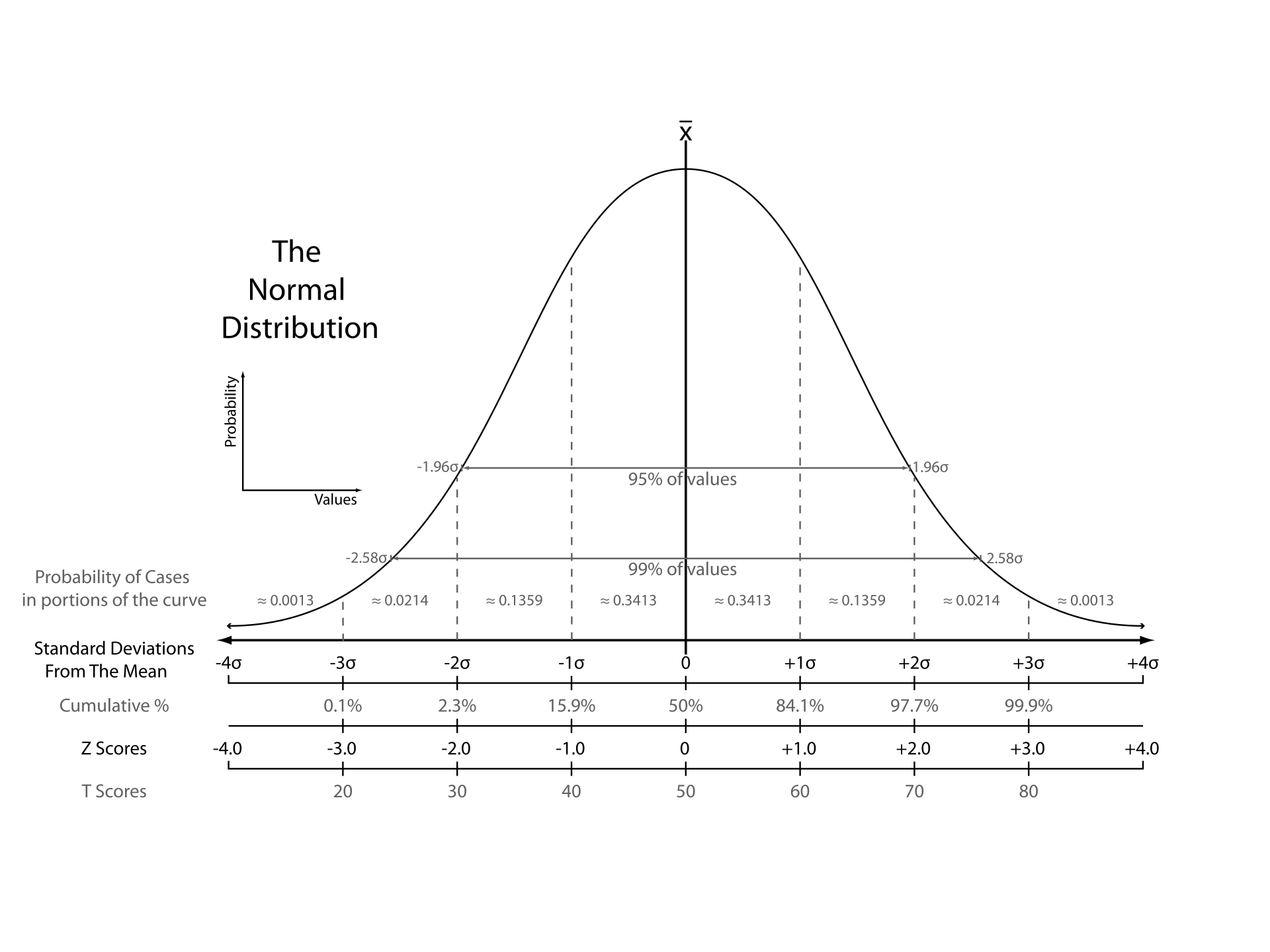Source: Wikipedia

As we can see, the probability to observe data point having z-scores beyond +/- 3 is extremely low (0.0026, i.e. 0.0013 * 2).
For that, a standard cut-off value for finding outliers are Z-scores of +/-3 or further from zero.

Pros of Z-scores:

Simple method when dealing with parametric distributions in a low dimensional setting.

Cons of Z-scores:

• This approach assumes data follow the normal distribution (if not may consider to transform the data)
  
• It can be used in multivariate settings
  
• If the distribution has outliers, the Z-scores will be naturally biased since it inflates the distribution’s parameters (mean and standard deviation) used to compute them.
  

The Tukey’s IQR approach quantifies the unusualness of an observation based on the IQR rule, according to which data point below (Q1-1.5*IQR) or above( Q3+1.5*IQR) have to be considered outliers.

The IQR method has two advantages over the Z-scores method:

• since it uses percentiles, it doesn’t rely on the assumption of a specific distribution.
  
• percentiles are relatively robust to the presence of outliers compared to mean-based methods.
  

• Probabilistic and Statistical Modelling: this is a parametric approach which assumes a specific probability distribution for data and estimates parameters of this distribution by using the expectation-maximization algorithm.
The estimated probability density function of this distribution gives the probability that an observation belongs to the distribution.
The smaller this value, the more likely that an observation is an outlier.

• Linear Regression Modelling: this is a multivariate parametric approach which models linear data correlations into a lower dimensional sub-space.
The distance of each observation from the estimated hyperplane, referred to as residual, quantifies its deviation from the model.
Residuals’ analysis allows to identify large deviations and outliers.

• Proximity-Based Models: this is a class of non-parametric unsupervised models which qualifies as outliers those observations that are isolated from the rest of observations.

This class can be further split into 3 categories of models:

• Cluster Based Models: Partitioning Cluster analysis (hierarchical clustering, k-means, PAM clustering). Normal data belong to large and dense clusters, whereas outliers belong to small or sparse clusters, or do not belong to any clusters
  
• Density Based Models: such as Density Based Clustering analysis (DBSCAN)
  
• Distance Based Models: such as K-nearest neighbours
  

Outliers Treatment

Once the outliers are identified, in order to choose how to handle them, we must understand which type of outliers we are dealing with.

• Error outliers, data points that lie at a distance from other observations because they are the result of inaccuracies, such as measurement or data entry errors.
• Sample outliers, data points that are not part of the same population as the rest of the sample.
• Interesting outliers, which are accurate data points that lie at a distance from other data points and may contain valuable information.

According to the type of outliers the possible approaches are:

1. If the outlier in question is an Error outlier, it should be corrected if possible. If not, it’s better to remove that observation.
2. If the outlier in question is a Sampling outlier, it is legitimate to remove it.
3. If the outlier is a natural part of the phenomenon under study and appropriately reflects the research question/phenomenon under study, it should be kept, even if it lies well outside the range of the other values for the sample and even if it reduces statistical significance. Indeed, excluding them will force the phenomenon to appear less variable than it is in reality, leading to distort results.
   
   When deciding to keep outliers, possible approaches are:
   - data transformation, by applying a mathematical function to all observed data points (e.g., to take the log) in order to reduce the variance and skewness of the data
   – data imputation, through some capping method such as Winsorization where all outliers are transformed to a value at a certain percentile of the data
   
   An alternative approach is to conduct the analysis both with and without the outliers and compare the differences

When deciding to remove outlier, it’s important to document which observations have been removed as well as for which reason.