Generalized Linear Models

6 minute read

Linear Models Limitations

A general linear model assumes that the response variable( $Y$ ) takes continuous values and that the error terms of the model are normally distributed with zero mean and constant variance

$\varepsilon \sim N(0,1)$

Although linear models provide a very useful framework, there are some situations where they are not appropriate and the relationship in the data cannot adequately be summarized by a simple linear equation, for two main reasons:

1. The dependent variable of interest may have a non-continuous distribution (i.e. the range value of the dependent variable is restricted).
2. The variance may be not constant.

For instance, when considering a Binomial distribution or a Poisson distribution the variance is a function of the expected value and therefore, for construction, it is not constant.

$X \sim B(n,p)\rightarrow E(X) = n , Var(X)=np(1-p)$

$X \sim P(\lambda)\rightarrow E(X) = Var(X)=\lambda$

Generalized linear models extend the general linear model framework to address both of these issues.

GLMs Characteristics

A generalized linear model is determined by three components:

the distribution of the target variable, which is assumed to be belong to the exponential family, a class of probability distributions which covers a large number of distributions such as Bernoulli, binomial, Poisson and also Gaussian distribution

the systematic component: any set of X = (X₁, X₂, … ,X_k) explanatory variables

the link function, which transforms the non-linear relationship between the expected value of the target variable and the predictors in a linear relation so that the target variable can be modeled with linear regression.

This article is focused on GLMs used to model binary or count data (i.e. when the response variables follows the binomial or Poisson distribution).

The table below describes those models’ structures

image-center

The multinomial regression model is an extension of the logistic regression model and it is used when the target is a categorical variable having multiple classes.

Logistic Regression

Logistic regression is the appropriate regression analysis to conduct when the target variable is dichotomous (i.e. it is a categorical variable having two classes 0 and 1).

For instance, logistic regression allows to answer a question such as:

How does the probability of heart disease (yes vs. no) change for every additional year of age of a person and for every pack of cigarettes smoked per day?

Logistic regression allows to predict the class of the target variable for a new observation by estimating the probability that that observation falls into the class 1 based on one or more independent variables (that can be either continuous or categorical).

Note that logistic regression does not return directly the class of observations. It allows us to estimate the probability (p) of class membership and then, on the basis of a given threshold, conclude that observations having a probability higher than the threshold will belong to the class 1.

Logistic Regression Assumptions

1. Logistic regression requires the dependent variable to follow a binomial distribution $Y \sim B(n,p)$

2. Independence of observations
This means that each observation is independent of the other observations; that is, one observation cannot provide any information on another observation.

3. No multi-collinearity
The independent variables should be independent of each other.

4. Equidispersion in data

Logistic Regression Link Function

Since the objective is to estimate a probability (i.e. a continuous but bounded value), model parameters must be estimated such as two conditions are met:
1. the estimated output cannot be negative (since it is a probability and it cannot be negative).
For that, the general linear model is modified by putting the linear equation in exponential form.
2. the estimated output can never be grater than 1 (since the probability cannot be greater than 1).
For that, the model output is divided by something bigger than itself.

Let $Y$ be the binary outcome variable indicating failure {0} or success {1}.

Let $X$ a vector containing a set of $k$ predictor variables.

In a logistic regression model, the probability of $Y$ to be 1, $p = P(Y=1)$ , is modelled by the following equation

$P(Y=1)=p=\frac{e^{\beta_{0} + \beta X}}{1+e^{\beta_{0} + \beta X}}$

Note that $p = P(Y=1)$ is nonlinear, which means that the effect of a change in $\beta_{k}$ will depend not only on $X_{k}$ (as in the classical linear regression), but also on the value of $X_{k}$ .

Even if it results a non-linear association, it is possible to model it in a linear way through a logarithmic transformation on the outcome variable probability, called logit, as follows

$logit(p) = log(\frac{p}{1-p})=\beta_{0} + \beta X$

where the term $\frac{p}{1-p}$ is the ODDS RATIO which represents the ratio of the probability of success over the probability of failure. That is to say that the probability of success is 0.50, then the odds of success is 1 to 1.

The logit transformation allows to link the expected value of the response variable to a linear combination of predictors.

Model’s parameters are estimated from the logit function via maximum likelihood method.

How to interpret logistic regression parameters

This task is quite more complex than for general linear regression, since model parameter are estimated on the scale of the model link function, i.e. the logit function

$logit(p) = log(\frac{p}{1-p})=\beta_{0} + \beta X$

To interpret model results, we need to come back to the scale of probabilities, so we need to calculate the exponential value of each model parameter $\large e^{\beta_i}$ .

The coefficient $i}$ means that for one unite increase in the $X_i$ variable, the odds to belong to the class 1 changes by a factor equal to $\large e^{\beta_i}$ .

The sign of the coefficient indicates whether the chance an observation to belong to the class 1 increases or decreases for the predictor $X_i$ .

The magnitude of the coefficient implies that for every one unit increase in in $X_i$ , the odds to belong to the class 1 changes by a factor equal to $\large e^{\beta_i}$ on average.

For example, if we are running a logistic regression to investigate how glucose level affects the probability to become diabetic and the regression coefficient for glucose is 0.052, it means that one unit increase in the glucose concentration will increase the likelihood of being diabetes-positive by $e^{0.052}$ times.

Using the Model to make Predictions

Once the logistic model estimated, the procedure to make prediction about new observations is as follow:

1. Predict the class membership probabilities of each observation based on predictor variables
2. Assign the observations to the class with highest probability score (i.e above 0.5)

Assessing Model Accuracy

The most commonly tool used to evaluate classification models is the Confusion Matrix.

In a confusion matrix, the actual and predicted values are organized in a tabular format as below

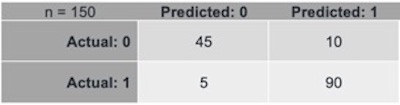
image-center

In this case, a total of 150 predictions have been made by using the model.

Out of those 150 cases, 100 observations have been predicted to belong to class 1 and 50 to the class 0. In reality, 90 observation belong to the class 1 and 45 to the class 0.

From this matrix, different metrics can be derived, such as:

True Positive (TP): the model predicts class 1 and the observation actually belongs to the class 1 (90 cases)
True Negative (TP): the model predicts class 0 and the observation actually belongs to the class 0 (45 cases)
False Positive (FP) (aka “Type I error”) : the model predicts class 1 but the observation actually belongs to the class 0 (10 cases)
False Negative (FN) (aka “Type II error”) : the model predicts class 0 but the observation actually belongs to the class 1 (5 cases)

The Accuracy of the model can be evaluated as $\frac{(TP+TN)}{Total}$ which describes, overall, how often the model predicts correctly.

Complementary to accuracy metric, there is the Total Error of the model $\frac{(TP+TN)}{Total}$ which quantifies how often the model makes a wrong prediction.

Poisson Regression

Poisson regression is used for modelling the number of events that occur in a given time period or area.

A Poisson regression is suitable when the target variable is a count variable that approximates the Poisson distribution. Thus, the possible values of $Y$ are the non-negative integers: 0, 1, 2 and so on.

However, the Poisson distribution assumes that events are rare (as opposed to more common events which tend to be normally distributed).
Therefore, Poisson regression is more suited to cases where the target variable takes small integer values.

One example of an appropriate application of Poisson regression is a study the number of failures for a certain machine at various operating conditions.

Explanatory variables, $X = (X_{1} , X_{2} , ..., X_{k})$ , can be continuous or a combination of continuous and categorical variables.

Poisson Regression Assumptions

1. The dependent variable follows a Poisson distribution

$Y\sim P(\lambda )\rightarrow E(Y)= Var(Y) = \lambda$

Furthermore, it is sometimes suggested that Poisson regression only be performed when the mean count is a small value.

2. Independence of observations
This means that each observation is independent of the other observations; that is, one observation cannot provide any information on another observation.

3. The mean and variance of the model are identical.
This is a consequence of Assumption 1 that there is a Poisson distribution. For a Poisson distribution the variance has the same value as the mean.

If this assumption is satisfied, we have equidispersion.

However, often this is not the case and the data is either under- or overdispersed with ove rdispersion the more common problem.

Overdispersion, can arise when one or more unobserved variables are contributing to the mean but are not included in the model. (If those variables were to be included in the regression, the variance would be reduced as the contribution to the residuals caused by their absence would be eliminated.)

Equidispersion assumption can be assessedby plotting model’s residuals

Poisson Regression Link Function

Since the aim of a Poisson regression is to model the conditional mean $E(Y|X_{k})$ or or the average number of events $\lambda$ , and since this value has to be a positive integer, model parameters must be estimated such as to be sure that the estimated value $E(Y|X_{k})$ is always positive.

For that, the general linear model is modified by putting the linear equation in exponential form.

$E(Y|X) = e^{\beta_{0} +\beta X }$

Let $Y$ be a Poisson outcome variable indicating the number of times that a certain event occurs during a given time period, with $E(Y) = \lambda$ .

Let $X$ a vector containing a set of predictor variables.

Then the Poisson regression of $Y$ on $X$ estimates parameter values for $\beta_{0}, \beta_{1}, ..., \beta_{k}$ via maximum likelihood method of the log link function, which allows to link the expected value of the response variable to the linear combination of predictors.

$log(Y|X )=log\lambda= \beta _{0} + \beta X$

This logarithmic transformation on the outcome variable allows us to model a non-linear association in a linear way.

Taking exponent on both sides of the equation returns the average number of time that a certain event occurs during a given time period

$E(Y|X )=\lambda= e^{\beta _{0} + \beta X}$

How to interpret Poisson regression parameters

After having carried out a Poisson regression, results have to be interpreted.
The aim is to determine which of the independent variables (if any) have a statistically significant effect on the dependent variable.

For that, we have to analyze the model parameters $\beta_{0}, \beta_{1}, ..., \beta_{k}$ .

Since model parameter are estimated on the scale of the model link function, i.e. the log function, to interpret model results, we need to come back to the scale of response variable, so we need to calculate the exponential value of each model parameter.

When the i independent predictor is a binary categorical variable, the parameter $e^{\beta_{k}}=\frac{ log\lambda_{group1}}{log\lambda_{group2}} = log\lambda_{group1} - log\lambda_{group2}$ represents the difference of the number of times an event occurs in one group versus another (e.g. number of car accidents amongst women and men). Therefore, if $\beta_{k}$ is positive we can say that the $E(Y)$ is $e^{\beta_{k}}$ times larger for the group 1 than for the group 2.

When the i predictor is continuous, if $\beta_{k}$ is positive, we can say that the $E(Y)$ is $e^{\beta_{k}}$ times larger when the variable $X_{i}}$ increases by one unit ( $e^{\beta_{k}} =\frac{ log\lambda_{X+1}}{log\lambda_{X}} = log\lambda_{X+1} - log\lambda_{X}$ ).

Enrica Zabaino